
Your Delivery is Stuck in Traffic. Could a Quantum Computer Clear the Way?
Ever wondered how the food you eat, the clothes you wear, the devices you use, or even the vehicle you drive make it to the market? How can you simply walk into a store and buy them, or better yet, have them delivered right to your doorstep?
There’s an entire process behind it, a massive web of complex routes, and tightly coordinated steps. Raw materials are sourced by one industry, transported to another for assembly, then to another for packaging, and finally delivered to distributors and retailers.
If you’ve never really considered that, maybe it’s time you do because it affects your life more directly than you think. If we can make this whole system faster, smarter, and more efficient, it will benefit everyone. This intricate, behind-the-scenes system is called logistics.
Sounds complicated? Don’t worry, we’ve got you. Let’s break it down with a simple analogy.
Think of logistics like your mom preparing a meal. She plans to go to the market, picking up vegetables and spices in one go, saving time and fuel. Then she prepares the meal and delivers it to you, hot and ready. But what if the vegetable shop and spice shop are never open at the same time? She now has to make multiple trips, wasting fuel, time, and energy.
If we extend this analogy a bit further, planning a meal is like how companies allocate tasks, figuring out how to get things done efficiently while saving time, money, and fuel. The market in our story is what the industry calls 'suppliers', places where raw materials come from. Cooking represents the processing stage, where raw inputs are turned into finished goods. And finally, just like your mom serves the meal, companies have to deliver their products, another stage that demands smart planning and careful use of resources.
Let’s hop into a big question: Why is logistics so important?
When we think of logistics, we often picture a delivery van or a warehouse. But it’s way more than that. Logistics covers everything, from getting raw materials to processing them, to making sure the final product reaches you on time. All of this happens while trying to use as little time, fuel, and money as possible. So whenever there’s a breakthrough in this field, it doesn’t just help one business; it sends shockwaves across entire economies and societies. Logistics isn’t just a background process; it’s the system that keeps industries flowing and connected. It's not just movement, it's momentum.
When Logistics fail, the world feels it. Take the pandemic, for instance, a time when the importance of logistics became crystal clear. Global lockdowns brought the entire supply chain to a halt. Goods couldn’t move. Shelves went empty. Industries paused. It was a wake-up call: logistics isn't just important, it’s critical to the functioning of the world.
Now, let’s use another scenario to deepen your understanding of the challenges logistics faces. Imagine you’re a business owner in your home country, and you need to make deliveries to several other countries. Each destination can be reached through multiple possible routes. Your task is to ensure on-time delivery to all locations, take the fastest possible paths, minimize fuel consumption, and use the least amount of resources, all while making sure you get back home efficiently. This challenge is a classic example of what’s known as the Traveling Salesperson Problem (TSP) a puzzle famous for being deceptively difficult to solve perfectly.
Sounds tough, right? However, finding the perfect solution requires evaluating a vast number of possibilities, a task that quickly becomes overwhelming for even the most powerful classical computers.
This raises a key question: how can we solve the problems plaguing our current logistics networks?
It’s something every business owner, every manufacturer, every stakeholder in the supply chain worries about. And now, a new player is entering the scene with the potential to reshape everything: quantum computing. Unlike classical computers, which check one solution at a time, quantum computers can process many possibilities simultaneously. They can evaluate all potential routes and constraints in parallel, quickly identifying the fastest and most resource-efficient delivery paths. This means smarter decisions, faster deliveries, and game-changing efficiencies that could lower costs for businesses and consumers worldwide.
Now, let's explore in more detail the TSP that we introduced in the last scenario.
The TSP is one of the most well-known and widely studied combinatorial optimization problems in computer science. Here's how it works:
You’re given a list of cities and the distances between each pair. Your task? Find the shortest possible route that allows you to visit each city exactly once and then return to your starting point.
Sounds familiar? It’s just like the global delivery scenario we discussed earlier. As the number of cities increases, the number of possible routes grows exponentially, making it incredibly difficult and time-consuming to solve using classical computers.
So, what makes the TSP so special? It belongs to a class of puzzles known as combinatorial problems, where the goal is to find the best possible arrangement or combination from an enormous number of possibilities.
To make this crystal clear, let's look at how the problem scales with a simple example. A route with just 4 cities has only 3 possible round-trip paths to check. But add just 11 more cities, for a total of 15, and that number explodes to over 43 billion (43,000,000,000). This "combinatorial explosion" is why these problems become impossible for even the fastest supercomputers.
On a more technical level, the Traveling Salesperson Problem is modeled as what's known as an "undirected weighted graph". Think of it as a map:
- The cities are the vertices (the points).
- The paths between cities are the edges (the lines connecting the points).
- The distance of each path is called the weight assigned to that edge.
The objective, in mathematical terms, is to find the single tour that connects all vertices with the minimum possible total weight. The image below visualizes this exact concept.

In this image, you can see:
- The black dots represent the cities (the vertices of the graph).
- The lines connecting them are the possible paths (the edges).
- Each line is associated with a distance or cost (the weight of the edge).
The challenge is to find a single route that visits every city just once and has the lowest possible total distance (weights), like the "Path 1" highlighted in red, dashe lines.
We saw earlier how the number of possible routes exploded to over 43 billion with just 15 cities. You might think, "Why does this matter? A computer is a machine; surely it can solve it eventually."
But add only a factor more cities and that’s not the case anymore. Solving this problem for many more cities on even the fastest supercomputer would take an impractically long time.
The problem mathematically is defined as one of the class of problems known as NP-hard. The "hard" part doesn't mean the math for one route is difficult; it refers to the mind-boggling task of having to check every single one of those billions of combinations to guarantee you've found the absolute best one.
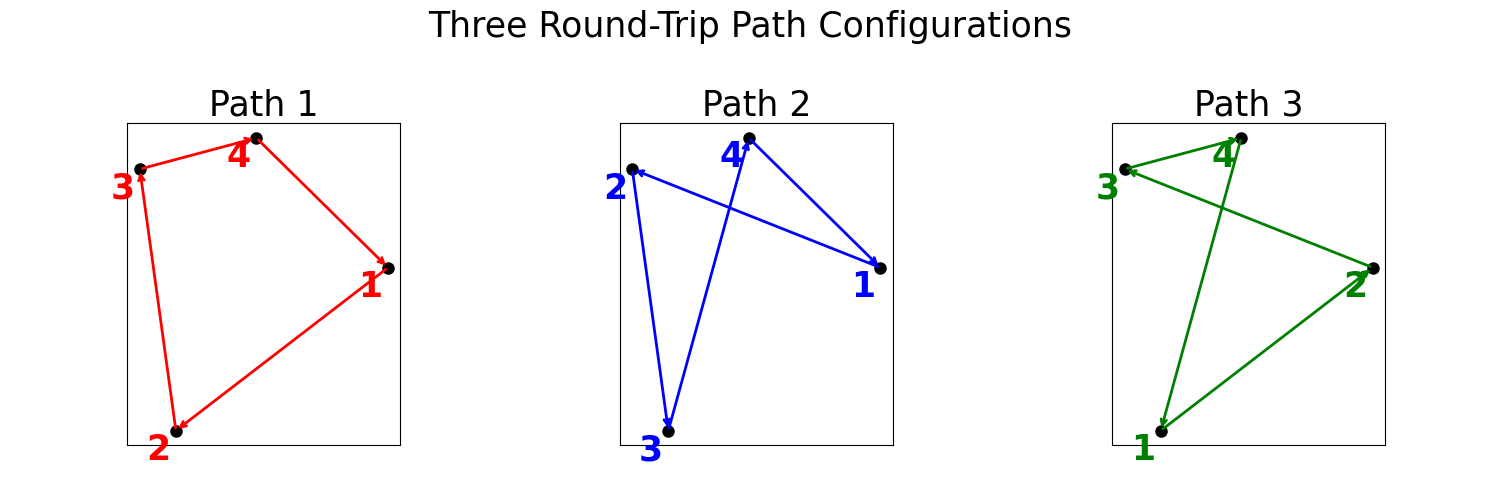
Another way to visualize this problem is to see the actual instructions a computer would use. Let's peek behind the curtain at a simple piece of code that builds the 'map' for our 4-city problem. The images below, which show the three possible round-trip routes for our 4-city problem, were generated using a simple Python script.
This helps us see exactly what a computer needs to evaluate. For anyone interested, the full code can be found in the appendix at the end of this article.
We've seen how to visualize this problem for a better understanding, but now let's explore something more interesting: how does a classical computer solve it?
One answer is a strategy called the "brute-force method." As the name suggests, this method involves raw computational power. The computer meticulously explores every single possible path, calculates the length of each one, and at the end, gives you the path with the shortest length.
Sounds simple, right? The problem isn't the logic, it's the scale. Even a few cities, like the 10 we used in our code, create a staggering 362,880 possible paths. A classical computer has to compute every single one, which takes a lot of time and is extremely inefficient.
To give you a better grasp of this, we solved the problem for 9 cities using the brute-force method on a laptop and plotted the results. The code checked every single one of the 40,320 possible paths to find the perfect solution.
So, you might be thinking, "If it solves the problem, why do we need another method?"
The limitation isn't about correctness; it's about time and scalability. While finding the best path for 9 cities is possible, in the real world, problems involve a much larger number of "cities." For those problems, the brute-force method would essentially take forever to compute a solution, making it completely impractical.
We've journeyed from our kitchens to the complexities of global supply chains and met the Traveling Salesperson Problem (TSP), a deceptively simple puzzle with world-altering implications. We've explored its technical side, modeling it as a graph, and understood its classification as an NP-hard problem, plagued by a "combinatorial explosion" that grows impossibly large.
We then looked at how a classical computer tackles this: the straightforward brute-force method. While it guarantees the perfect solution, our own simulations showed its fatal flaw. Checking every single path works for a handful of cities, but the time required skyrockets exponentially, quickly becoming impractical for real-world logistics challenges. Clearly, brute force isn't the answer.
So, how do we find efficient routes if every possibility is checked off the table? Is there a smarter way?
In our next article, we'll dive into the clever world of heuristic algorithms, advanced classical methods like simulated annealing that use intelligent shortcuts to find excellent solutions quickly. We'll explore how they work, see their strengths and weaknesses with more hands-on examples, and ultimately ask: are even these powerful methods enough?
To explore the code used in this article and follow along, check out our GitHub repository: https://github.com/SchoolofQuantum
Join us in Part 2 as we continue our quest for the ultimate optimization solution!
Written by Dhruv Sachdeva and Dr. Jonas Kölzer


Code available on GitHub:
https://github.com/SchoolofQuantum/Quantum-TSP